Modern x-ray and neutron diffraction techniques can give precise parameters that describe dynamic or static displacements of atoms in crystals. However, confusing and inconsistent terms and symbols for these quantities occur in the crystallographic literature. This report discusses various forms of these quantities, derived from probability density functions and based on Bragg diffraction data, both when the Gaussian approximation is appropriate and when it is not. The focus is especially on individual atomic anisotropic displacement parameters (ADPs), which may represent atomic motion and possible static displacive disorder.
The first of the four sections gives background information, including definitions. The second concerns the kinds of parameters describing atomic displacements that have most often been used in crystal structure analysis and hence are most commonly found in the literature on the subject. It includes a discussion of graphical representations of the Gaussian mean-square displacement matrix. The third section considers the expressions used when the Gaussian approximation is not adequate. The final section gives recommendations for symbols and nomenclature.
We are especially indebted to Verner Schomaker for his critical reading and
counsel on many drafts of this Report, to Hans Boysen for his special help
with Section 3, and to Richard Marsh, Emily Maverick and Tullio Pilati for their
advice.
There are four main sections. The Introduction continues, after the present subsection, with a discussion of the rationale for and genesis of the Subcommittee that wrote this report (Subsection 1.2), notation for position and displacement vectors (1.3), a consideration of the structure factor and atomic displacements (1.4), and comments about the terminology to be used (1.5).
The second main section, Displacement Parameters Based on the Gaussian Approximation, concerns the kinds of parameters describing atomic displacements that have most often been used in crystal structure analysis and hence are most commonly found in the literature on the subject. Its subsections are: 2.1, Anisotropic displacement parameters, which includes a discussion of the common symbols used; 2.2, Equivalent isotropic displacement parameters; and 2.3, Graphical representations of the Gaussian mean-square displacement matrix.
The third main section, Beyond the Gaussian Approximation, considers the expressions used when the Gaussian approximation is not adequate. Our Recommendations for nomenclature are in the final main section.
Anisotropic displacement parameters (ADPs) (see the discussion of terminology
in subsection 1.5 and of symbols in subsection 2.1) have typically been
determined and reported in the crystallographic literature in a variety of
ways, symbolized sometimes as U (as in 
or 
), sometimes
as B (as in 
or 
), and sometimes as 
(as in 
). Unfortunately, these terms have not always
been used consistently.
Dimensionless quantities, e.g., the , have been
misidentified as values, which are of dimension (length)2. When
these and related quantities were first determined more than four decades ago,
they were considered at best to have qualitative significance, and
inconsistencies, when noticed, were often disregarded. Cruickshank's (1956)
papers marked a turning point toward quantitative interpretation in terms of
simple physical models. Since then, technical improvements, both in the
measurement of diffraction data and in computing, have led to increased
physical significance in the experimentally determined ADPs. The fact that
these quantities are now more meaningful,
and the lack of uniformity with which they
have been presented, have been discussed informally in recent years by more
than one IUCr Commission, but no consensus has previously been reached on an
acceptable form of presentation. This situation was brought recently to the
attention of the Commission on Crystallographic Nomenclature. That body
established this Subcommittee, charging it with examining the merits of
adopting a
uniform approach to reporting in structural papers quantities that describe
atomic displacement, and with making such recommendations as might be deemed
appropriate. Discussion within the Subcommittee,
conducted principally through electronic correspondence, identified two major
areas
in which uniform definitions,
terminology, and nomenclature would be desirable. These include anisotropic
displacement parameters in the Gaussian approximation and in situations in
which the Gaussian approximation is inadequate. In considering the
uncertainties of experimentally determined ADPs, the reader is referred to
the Report of a Working Group on the Expression of Uncertainty in
Measurement (Schwarzenbach, et al., 1995), appointed by the IUCr
Commission on Crystallographic Nomenclature, which discusses the general
concept of uncertainty in the result of
a crystallographic measurement, and its application.
The recommendations at the end of this report are proposed for use in all future publications of the International Union of Crystallography. Authors of structure refinement programs, particularly those in widespread use, are encouraged to bring their programs into full conformity with these recommendations.
Recommendations on the nomenclature of thermal
diffuse scattering [e.g., Willis (1993)] and disorder diffuse
scattering [e.g., Jagodzinski & Frey (1993)] were considered as
outside the scope of this report.
Some notation to be used in this report for basis vectors
and their components is summarized here. The local instantaneous
atomic position vector is denoted by r+u, with
r the mean atomic position vector and u the displacement
vector of an atom from its mean position. We use the symbols 
, and 
, as is common, for the lengths of the reciprocal axes.
Quantities referred to the direct lattice basis, a,
b, c (or equivalently 
)
:
Components of r: x, y, z (or equivalently 
).
Components of u: 
(or
equivalently 
).
Related anisotropic displacement parameter: 
; (dimensionless).
Quantities referred to the basis 
(or equivalently 
):
Components of r: 
(or equivalently 
).
Components of u: 
(or
equivalently 
).
Related anisotropic displacement parameter: 
; (length)2.
Quantities referred to the Cartesian basis 
):
Components of r: 
(or
equivalently 
).
Components of u: 
(or equivalently 
).
Related anisotropic displacement parameter: 
;
(length)2.
The structure factor of reflection h is given in a fairly general form by the Fourier transform of the average density of scattering matter
with the integration extending over the repeating structural motif,
confined to
a single unit cell. The brackets denote a double averaging over the possible
displacements of the atoms from their mean positions - a time
average over the atomic vibrations in each cell, followed by a space average
that consists of projecting all the time-averaged cells onto one and dividing
by the number of cells, h is a diffraction vector obeying the
Laue equations, and 
is the static density of the motif,
consistent with
the instantaneous local configuration of the nuclei in a unit cell.
To reduce the above general picture to what is used in conventional crystal structure analysis, we first assume that the average density of matter in (1.4.1) can be regarded as a superposition of averaged atomic densities. This so-called isolated-atom approximation is essentially equivalent to assuming independently displaced atoms, a fair initial approximation, although not generally valid. The average density of scattering matter at the point r in a unit cell can then be approximated as
Here N is the number of atoms in the unit cell,
is the occupancy factor of the kth atom,
is the density (electron
density for X-rays, or a delta function weighted with the scattering length
for neutrons) due to atom k at a point r when the
nucleus of atom k is at 
, and
is the probability density function (pdf)
corresponding to the probability for having atom k displaced by
the vector ( - 
) from its reference position
in an average unit cell, which will be the mean position if
is sufficiently symmetrical. It is
important to remember that
the approximations in (1.4.2) include the assumption that atoms are
not deformable, by bonding or otherwise, even though at this stage the
static atomic electron density, , has not
been assumed to be spherically symmetrical.
If eq. (1.4.2) is now substituted into eq. (1.4.1), and the order of the summation and integration is interchanged, the structure factor becomes
with
If the substitutions 
and 
are made, the integral in (1.4.4) becomes
The inner integral in (1.4.5) has the form of a conventional
convolution of the density of atom k with the pdf for a displacement of this
atom from its mean position; the outer integral is a Fourier
transform of this convolution. This transform is multiplied by an exponential
that depends on the mean position, , of atom k.
By the convolution theorem, the Fourier transform of a convolution equals the product of Fourier transforms of the functions involved. When this theorem is applied to the outer integral in (1.4.5), we obtain the conventional approximation for the structure factor of a Bragg reflection
If we let 
and (as before)
, then in (1.4.6)
is the scattering factor or form factor of atom k (for neutrons this
is replaced by the
scattering length ), and
is the Fourier transform of the pdf, 
, for the displacement of the kth
atom from its reference position, r 
. This term contains the
dependence
of the structure factor on atomic displacements, and has been known by the
names ``atomic Debye-Waller factor" and ``atomic temperature factor"
(see section 1.5). There are no restrictions on the functional form of
the pdf in the integrand of (1.4.8).
Let us now recall that the structure factor equation used in routine refinement of atomic parameters is further simplified in two ways:
First, for X-rays, the static atomic electron density is assumed to have spherical symmetry. This reduces the atomic scattering factor to the form
which has been computed and extensively tabulated for all the neutral elements and many ions (Maslen, Fox & O'Keefe, 1992). The spherical-atom approximation necessarily removes fine details of the (calculated) electron density, but may be used routinely, and serve as a starting point for more refined determinations of atomic positions and studies of charge density (e.g., Coppens & Becker, 1992; Coppens, 1993).
Second, the pdf for atomic displacement is most frequently approximated by a
univariate or trivariate Gaussian, depending on whether the atomic
displacements are
assumed to be isotropic or anisotropic respectively. If a trivariate Gaussian
is assumed, and the atomic subscript k is omitted,
the resulting expression for 
from (1.4.8) is
Equation (1.4.10) can be derived from the theory of lattice dynamics in the
harmonic approximation, which considers only the (always present)
contribution of motion to the atomic displacement (e.g., Willis & Pryor,
1975). However, this equation may also be applied to static displacive
disorder. The form of the atomic Debye-Waller factor, ,
represented in (1.4.10) is the most common one in standard structure
refinements and will be discussed in Section 2. Various other approximations
have been proposed for situations in which the Gaussian formalism is not
adequate, e.g., when the anharmonic contribution to the crystal dynamics
is significant; the most common are discussed in section 3.
We present now a short discussion of common variants of eq. (1.4.10), which can be rewritten as
This shows that the exponent is proportional to minus the mean-square
projection of the atomic displacement u on the direction of the
diffraction vector h times the squared magnitude of h.
If we denote the projection of u on the direction of h by
, and make use of the relation:
, (1.4.11) becomes
As long as the atomic displacements are anisotropic, the value of the average
in (1.4.12) depends on the direction of h. This is then the
anisotropic Gaussian Debye-Waller factor, , which is discussed in
detail in Section 2. If, however, the atomic displacements are isotropic, the
average in (1.4.12) is a constant determined by the structure alone, but
possibly different for non-equivalent atoms, and the left-hand side of this
equation no longer depends on the direction of h, but only on its
magnitude. This is then the atomic isotropic Gaussian Debye-Waller factor,
The lowest-order approximation to is the overall isotropic
Debye-Waller factor. It has the same form as (1.4.13), and presumes that
all the atoms have the same isotropic mean-square displacement,
. The whole crystal structure is assigned, in this
approximation, a single displacement parameter. This approximation is
used in initial
stages of crystal structure determination by direct methods.
We conclude this section with some remarks on the structure
factor for electron diffraction by a crystal. The density of scattering
matter, 
, is here interpreted as the distribution of electrostatic
potential within the unit cell. This potential is then approximated by a
superposition of electrostatic potentials contributed by individual
atoms, and the effects of motion are taken into account, as for
X-rays and neutrons, by the convolution of the potential of
an atom at rest with the probability density function describing the
atomic motion (e.g., Vainshtein and Zvyagin, 1993). The atomic
(spherical) scattering factor for electron diffraction, 
, for an atom at rest and diffraction vector 
, is related to
that for X-rays by the Mott formula (e.g., Vainshtein, 1964) which
has the form
with 
the atomic number and 
is the X-ray
form factor of atom k [see (1.4.9)]. This formula,
with the correct proportionality constants, has been used along with
other techniques in extensive tabulations of spherical form factors for
electron-diffraction (see, e.g., Cowley, 1992). The Debye-Waller
factor, here expressing the `smearing out' of the electrostatic potential,
is given by the same expression as that quoted above for X-rays and neutrons
(e.g., Vainshtein, 1964; Vainshtein & Zvyagin, 1993). The structure
factor for electron diffraction is therefore analogous to that
appearing in (1.4.6) but is often given in a different notation.
The quantity T that occurs in eq. (1.4.6) has been commonly referred to either as the Debye-Waller factor or the temperature factor because Debye (1913) and Waller (1923) first understood and formulated the effect that thermal vibrations would have on the intensity of X-ray scattering. It has, however, long been recognized, as discussed in section 1.4 above, that static displacements would have a similar effect. We therefore avoid the term ``temperature factor", and recommend that others do so also, in part because of this ambiguity about the origin of the atomic displacements that cause the diminution in scattering. Another reason for avoiding the phrase ``temperature factor" is the confusion caused by the fact that it has not infrequently in the past been used for terms in the exponent in expressions like that on the right side of eqs. (1.4.12) and (1.4.13), rather than for the entire exponential multiplicative factor.
A detailed treatment of the physical background of possible atomic displacements is quite beyond the scope of this report. However, we shall try to summarize and describe briefly the most important components of the displacement. The best known is the displacement arising from atomic vibrations. When these result from the motion of molecules or molecular fragments (e.g., Willis & Pryor, 1975), they are usually characterized by relatively large amplitudes. In crystals containing relatively strongly bonded atoms (e.g., molecular and ionic crystals), much smaller displacement amplitudes result from the ever-present internal vibrations, such as bond stretching and bending (e.g., Wilson, Decius, & Cross, 1954). All of these motions are temperature-dependent, unless the temperature is very low. Other effective displacements from the mean position may arise as a result of a variety of possible types of disorder. These include small deviations from ideal periodicity, present in all real crystals; orientational disorder, present in many molecular crystals; density and displacement modulations; and short- and long-range displacive correlations. Many types of disorder give rise to diffuse scattering, which can often be analyzed (e.g., Jagodzinski & Frey, 1993). There are, in addition, numerous other possible contributions to apparent displacements, one of the most important of which is use of an inadequate model, e.g., inadequate absorption correction, or use of a Gaussian probability density function when it is inappropriate.
In view of the large number of possible causes of an apparent
atomic displacement, we recommend expanding the definition of ``Debye-Waller
factor" to include displacements arising from any source. We will use
the term ``Debye-Waller factor"
when we mean the entire factor that multiplies the scattering factor of
an atom at rest, and recommend that this term be
used when words are wanted to refer to the quantity , or
T, that occurs in equations such as (1.4.6), (1.4.8), and
(1.4.10) through (1.4.13).
There was considerable discussion in our Subcommittee concerning the proper words to use when referring to the terms in the exponent that are variables during a typical least-squares refinement to fit a structural model to intensity data. These terms are formulated and symbolized in various ways, discussed in detail in section 2.1 below. We recommend unanimously the term ``displacement parameters" (often ``anisotropic displacement parameters", or ADPs) to describe these quantities. Two of us initially favored ``displacement coefficients", believing that once refinement is completed, this term is more appropriate, but were persuaded that current usage strongly favors the recommended term, ``displacement parameters".
As discussed in section 1.4 above,
diffraction studies yield information not only about mean atomic
positions but also about the probability density functions (pdf's) of atomic
displacements from these mean positions. If the atomic pdf is assumed to
be a trivariate Gaussian, the characteristic function
corresponding to this pdf - by definition, its Fourier transform - can
be described by the second moments of the pdf, which in the present
context are called anisotropic mean-square displacements. If
not, higher cumulants of a non-Gaussian pdf can, in principle, also be
determined; these are simple functions of moments (e.g.,
Kendall & Stuart, 1977), but there are difficulties. For
example, these higher terms are only likely to be important when the
second moments of the pdf's are relatively large. However, as can be seen
from the basic expression for the isotropic Debye-Waller factor,
,
the larger the second moment, the
more rapidly the scattering from the atomic center in question falls off with
increase in the scattering angle. Thus, just when the higher terms
become important, they become difficult to measure, for lack of
contribution by the scattering center to the Bragg intensities.
The mean-square displacements, which define the pdf in the various Gaussian approximations, used to be known as atomic vibration parameters or thermal parameters but have recently been designated as atomic displacement parameters, isotropic or anisotropic, to allow for the effects of static displacive disorder, as well as for those of the always-present atomic motion. There exists an extensive literature on the interpretation of these parameters (e.g., Dunitz, Schomaker & Trueblood, 1988, and references cited therein).
The purpose of this section is to relate alternative forms of anisotropic displacement parameters (ADPs) to the expression for the Debye-Waller factor that is valid within the framework of the assumptions underlying the harmonic approximation (e.g., Willis & Pryor, 1975). We also discuss anisotropic displacement parameters in relation to different coordinate systems, outline the transformation properties of the resulting quantities, present several forms of equivalent isotropic displacement parameters, and describe briefly graphical representations of the Gaussian mean-square displacement matrix.
The usual expression for T(h) is [eq. (1.4.10) restated]:
These fundamental equations take on different forms according to the basis vectors to which we refer the diffraction and displacement vectors. In carrying out coordinate transformations in the formalism of tensor algebra, quantities that transform like direct basis vectors are called covariant and are indicated by subscripts, while quantities transforming like reciprocal basis vectors are called contravariant and are indicated by superscripts. The direct and reciprocal bases are not necessarily those of the corresponding lattices; they may be any pair of dual bases. Let us first assume that the diffraction vector is referred to the basis of the reciprocal lattice and the atomic displacement vector to the basis of the direct lattice, as follows
and
Note that the components of h and u are dimensionless. The first scalar product appearing on the right-hand side of eq. (2.1.15) can now be evaluated as
and similarly
We used here the definition of the dual (direct and reciprocal) bases:
If we insert eqs. (2.1.18) and (2.1.19) into eq. (2.1.15)
we obtain for
with
The quantity 
defined by eqs. (2.1.21) and
(2.1.22) is one of
the frequently employed forms of the anisotropic displacement parameter;
note the use of superscripts for the indices, since the
components of are contravariant.
For an atom, each component is
2 
times an average of a product of two
components of an atomic displacement vector, when the latter is referred to
the basis of the direct lattice.
We shall now retain h as defined by eq. (2.1.16), but redefine u as follows
The components of u in this representation, 
, have
dimension
length, and the basis vectors 
are dimensionless (see, e.g., Hirshfeld & Rabinovich, 1966).
Only in orthorhombic, tetragonal and cubic crystal systems must these basis
vectors be mutually orthogonal unit vectors, i.e., orthonormal,
since it is only in these systems that the equalities 
,
,
and 
are necessarily true. The departures of these basis
vectors from orthonormality in other systems are associated with the
departures of the angles 
, 
, and 
from 90 
. If we
now repeat the evaluation of the scalar products in eq. (2.1.15) with
h given by eq. (2.1.16) and u given by eq. (2.1.23),
we obtain for T
with
another well known form of the ADP. This
form is often preferred because the elements of the
tensor
U have
dimension (length)2 and can be directly associated with the
mean-square displacements of the atom considered in the corresponding
directions. Note in particular that the mean-square displacement in an
arbitrary direction denoted by the unit vector n, when n
is referred to unit vectors parallel to the reciprocal
basis vectors so that its components are covariant, is given by 
(see section 2.3.2).
In any event, the dimensionless elements of
are also correctly associated with the general expression
for T(h), given by eq. (2.1.15).
Another form of the anisotropic displacement parameter, which is used in some conventional refinement calculations, especially in biomolecular crystallography, is
and the corresponding expression for T becomes
Since B and U are equivalent, apart from a constant factor, and U has a more direct physical significance than B, we recommend that the use of B be discouraged.
A brief discussion of the transformation properties of
and U may be helpful. The
corresponding representations of the atomic displacement vector are
and
respectively (Hirshfeld & Rabinovich, 1966). If the basis of the direct lattice is changed in some manner, the new components of the displacement vector u are related to the old ones by linear transformations, say
and
The elements of the transformation matrices depend on the old and new bases.
It follows from eqs. (2.1.22) and (2.1.25) that and U transform as products of the corresponding components of
the displacement vector. Hence, the transformation rules for and U become
and
and thus conform to those valid for tensors of the second order (e.g.,
Spain, 1956). The transformation matrices R and Q are obviously
different, since the basis vectors to which u, in its two representations,
is referred depend in a different manner on the basis of the direct lattice .
This transformation property will be illustrated in detail in section 2.1.2
by the orthogonalization of and U.
We comment finally on the form of the Debye-Waller factor when both the
diffraction vector and the atomic displacement vector are referred to
the same Cartesian basis, say 
, 
, 
.
It is understood that the use of this representation is usually, in
crystallographic practice, preceded by appropriate transformations (see
below for a detailed example).
The h and u vectors, in the Cartesian representation, are given by
and
All the indices are given here as subscripts, since in the Cartesian representation the position of the indices is irrelevant. Note that the components of h in eq. (2.1.34) have dimension (length)2. The scalar products in eq. (2.1.15) are now readily evaluated and we obtain for the Debye-Waller factor
with
an element of an atomic mean-square displacement tensor, with dimension (length)2, referred to a Cartesian basis. This representation avoids the hazards associated with calculations in oblique coordinate systems and is used almost always in lattice-dynamical studies and thermal motion analysis, and very often in constrained refinement of atomic parameters.
(for a given atom) do not
represent different tensors, just different sets of components of the
atomic quadratic mean-square displacement tensor. They can be interrelated by
transformations converting sets of components of a tensor into each other
(e.g., Spain, 1956). Frequently, however, the phrase ``set of
components of a tensor" is abbreviated as ``tensor". This practice
is followed here and U, , and B are sometimes
referred to as tensors.
The displacement parameters , , and ,
given by eqs. (2.1.22), (2.1.25), and
(2.1.26), are so closely related that the use of all of
them in the crystallographic literature is not only
unnecessary, but conducive to confusion. The
relationships needed are shown in a single equation, obtained by comparison of
eqs. (2.1.21), (2.1.24) and (2.1.27):
It is true
that fewer arithmetic operations are needed to compute T from
than from 
, but with the advent of computers this
advantage has become negligible.
Referring an ADP tensor to a Cartesian basis is somewhat less simple. We proceed to show how this is done, both in order to illustrate the above-outlined transformation of tensors and to provide some background for the following section.
Construct a Cartesian system by taking, for example,
along a, along 
, and along
the vector product 
. The resulting
vectors
comprise an appropriate and common orthonormal set of basis vectors.
Eqs. (2.1.35) and (2.1.17) are both expressions for u. Hence
If we take the scalar products of the left-hand side and right-hand sides of
eq. (2.1.40) with , and , we
obtain three linear equations, or a matrix equation of the form
This is a transformation of the components of u, referred to the basis of the direct lattice, to its Cartesian components. The transformation matrix can be evaluated once the Cartesian basis vectors are defined (e.g., as above). If we adopt the index notation in the second line of eq. (2.1.17), eq. (2.1.41) can be written as
with
We can similarly transform a product of components of u between the lattice and Cartesian bases, and finally an average of such a product:
If we now make use of eqs. (2.1.22) and (2.1.37) we obtain
which is the expression for the transformation of
to Cartesian coordinates.
The orthogonalization of U proceeds along similar lines. The required version of eq. (2.1.40) is now [cf. eq. (2.1.23)]
and following the same procedure by which eq. (2.1.41) is obtained, we arrive at the transformation
which relates the components of u, referred to the 
basis, to its Cartesian components. Equation (2.1.46)
can be written concisely as
with
an element of the matrix product appearing in eq. (2.1.46). The desired transformation is obtained analogously to eq. (2.1.44) as
with 
and
.
The explicit form of the transformation matrix appearing in eq. (2.1.41), for the specific Cartesian basis defined in eqs. (2.1.39), is:
Of course, a Cartesian basis associated with the direct and/or reciprocal bases can be chosen in an unlimited number of ways. A more general discussion of the construction of such Cartesian bases is given elsewhere (Shmueli, 1993).
It was pointed out by Hamilton (1959) and by Willis & Pryor (1975) that for minor departures from isotropic motion, or for anisotropic displacement parameters deemed to be physically insignificant, it may be worthwhile to replace the six-parameter description of anisotropic motion by a single quantity, which should describe an isotropic equivalent to the weakly or dubiously anisotropic case.
The IUCr Commission on Journals (1986) recommended that ``equivalent isotropic displacement parameters" be computed from the expressions proposed by Hamilton (1959) and by Willis & Pryor (1975). However, a number of different incorrect expressions have also been used (Fischer & Tillmanns, 1988), and this has led to considerable confusion. We first review the proper definitions and demonstrate their equivalence.
The first definition of the equivalent isotropic displacement parameter, as given by Hamilton (1959) and Willis & Pryor (1975), is
with 
an element of a mean-square displacement tensor, referred
to a Cartesian basis [see eqs. (2.1.34) - (2.1.37)].
The trace of 
, as given on the right-hand side
of eq. (2.2.51), is equivalent to the sum of the eigenvalues of this
matrix. These eigenvalues are often computed,
since an eigenvalue of the matrix represents the
mean-square displacement along the corresponding eigenvector.
The right-hand side of eq. (2.2.51) can then be interpreted as a
mean-square displacement averaged over all directions.
Equation (2.2.51) can thus be applied to the computation of
either by taking the trace of , which was obtained from
eq. (2.1.44) or eq. (2.1.49), or by using the sum of the
eigenvalues of . However, it is essential to note that
eq. (2.2.51) holds only for the Cartesian displacement tensor
. It will give incorrect values of if U
is referred to oblique basis vectors and its trace taken instead of
that of .
Since the basis vectors of the Cartesian system have the property
, a consideration of eqs.
(2.1.35), (2.1.37), and (2.2.51) readily leads to
This equation is a convenient starting point for testing the equivalence of
various definitions of . The second definition by Willis
& Pryor (1975) is the first line of the next equation
with g the real space metric tensor. This shows that eqs.
(2.2.51) and (2.2.53), the two recommended definitions of
, are equivalent.
If we make use of eqs. (2.2.54) and (2.1.38), two additional
expressions for can be obtained:
and
Thus, eqs. (2.2.51), (2.2.54), (2.2.55), and
(2.2.56) are equivalent representations of the equivalent isotropic
mean-square displacement parameter , obtainable from the commonly
employed anisotropic displacement parameters.
We can also arrive at eq. (2.2.54) by directly combining eqs. (2.1.44) and (2.2.51), and making use of a known property of the matrix A. We have
since
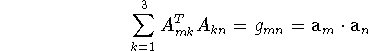
(e.g., Prince, 1982). This derivation shows that the value of
does not depend on the particular
form of the matrix A, which transforms the components of u from
the lattice to the Cartesian basis.
Acta Crystallographica requires that published values of
be accompanied by an evaluation of the standard deviation (now standard
uncertainty) in these quantities. The calculation of this estimate is
described in detail by Schomaker and Marsh (1983). A useful measure of
the anisotropy of the mean-square displacement tensor is the ratio of its
minimum and maximum eigenvalues. We recommend that published or
deposited values of be accompanied by both the standard
uncertainties and the ratio of the minimum to the maximum eigenvalues
of the corresponding anisotropic displacement tensors. Both the
uncertainty of and the ratio may be
helpful in judging the extent to which the use of is justified.
Just as interatomic distances in crystals are most conveniently discussed in
terms of atomic coordinates such as 
with dimension
length rather than in terms of the dimensionless components 
, the
physical interpretation of atomic displacement parameters is most convenient
in terms of the mean-square displacement matrices U with elements having
dimension (length)2 .
In the absence of anharmonicity, the anisotropic mean-square displacement matrix U can be regarded as the variance-covariance matrix of a trivariate Gaussian probability distribution with probability density function
Here x is the vector of displacement of the atom from its mean
position, and 
is the
inverse of the quantity defined by eq. (2.1.25).
If the eigenvalues of 
are all positive, then the surfaces of
constant probability defined by the quadratic forms
are ellipsoids enclosing some definite probability for atomic displacement.
This is the basis for the ORTEP ``vibration ellipsoids" (Johnson, 1965) that
are used in so many illustrations of crystal structures. The lengths of the
principal axes of the ellipsoids are proportional to the eigenvalues of the
matrix expressed in the appropriate Cartesian system, and the
directions of the principal axes correspond to the eigenvectors of this
matrix. This representation cannot be used when has one or more
negative eigenvalues, because the resulting non-closed surfaces are no longer
interpretable in terms of the underlying physical model.
The mean-square displacement amplitude (MSDA) in a direction defined by a unit vector n is
with n referred to the unit vectors 
, 
, parallel to the reciprocal vectors
, ,
respectively. The bases 
and 
are mutually reciprocal (Hirshfeld & Rabinovich, 1966). Note that
whereas 
in eq. (2.3.59) is
dimensionless, has dimension
(length)2 . As
n varies, the surface generated by is not an
ellipsoid; it is usually peanut-shaped.
Such surfaces can be constructed even for non-positive-definite tensors and
they are therefore particularly useful for inspecting difference tensors
between experimental tensors and those obtained from
kinematic or dynamic models of atomic and molecular motion (Hummel, Raselli
& Bürgi, 1990).
The distinction between the surfaces defined by eqs. (2.3.2) and (2.3.3) has often proved puzzling. Note that the right-hand side of (2.3.2) is a constant, the (arbitrarily chosen) equi-probability level for defining the ORTEP ellipsoids. When the matrix of the mean-square displacement tensor is non-positive definite, the quadratic surface defined by (2.3.2) is no longer closed, and no ellipsoid can be plotted. In contrast, the right-hand side of (2.3.3) is the mean-square displacement amplitude (MSDA) in a given direction, and varies as n varies. Only positive values of the quantity defined in (2.3.3) are meaningful for an individual atom, but negative values can be meaningful when differences in MSDA values are calculated. The MSDA surfaces can be plotted with the aid of the program PEANUT of Hummel et al. (1990); negative values are plotted as dashed contours.
The situation is less straightforward if the distribution function
is not Gaussian. A large variety of different approximation formalisms, as well
as different nomenclature for similar formulations, is found in the literature.
Summaries have been given by Johnson & Levy (1974), Zucker & Schulz (1982),
Coppens (1993), and Kuhs (1992). By virtue of eq. (1.4.8), one may
express
either pdf(u) or as a series expansion and obtain the other
quantity by Fourier transformation.
The most widespread approaches are based on formalisms developed in
statistics to describe non-Gaussian distributions (Johnson, 1969). They use a
differential expansion of the Gausssian pdf. Two formulations are found in
frequently used refinement programs, the cumulant or Edgeworth
expansion
and the quasi-moment or Gram-Charlier expansion
with 
the Gaussian Debye-Waller factor (see sections
1.4 and 2.1) and 
, 
, ... the third, fourth,
... order (anharmonic) tensorial coefficients. There are in general ten
cubic, fifteen quartic, ... terms that enter into the treatment. In
statistics they are called
cumulants and quasi-moments, respectively. They constitute the parameters of
the refinement. Various symbols for these coefficients are scattered through
the literature. Greek letters are chosen here to comply with the
's of the Gaussian case, which may thus be considered as
second-order coefficients. For the same reason the factors 
,
with N the order of the tensor, are included, also to follow standard
physical notation, which uses 
as the scattering
vector. The factors 
and/or the factors 1/N!
(e.g., Kuhs, 1992)
are sometimes omitted in the literature. For comparability of future
results, it is therefore proposed that only coefficients defined as in
(3.1.61) and (3.1.62) be published, and that subscripts be used
to indicate the type of expansion employed.
The , , ... are dimensionless quantities. As
proposed by Kuhs (1992), they may be transformed to quantities of dimension
(length)N by
with to be replaced by , 
... Note that this is a
generalization of eq. (2.1.38). It must be stressed, however, that
the , , ... are simple expansion coefficients
and (in general) have no direct physical meaning. The transformation
(3.1.63) thus has no such merits as in the Gaussian case, and some
real-space illustrations should always be given to permit the results to be
appreciated. The best way is certainly to plot the corresponding pdf,
obtained by inversion of (3.1.62) or (1.4.8). Only programs
that produce sections
of the pdf's seem to be currently available, although a three-dimensional
visualisation similar to ORTEP would be highly desirable. Another way of
presenting the results is by tensor contraction (Kuhs, 1992). For even-order
terms, full contraction yields an invariant scalar,
For the Gram-Charlier series, this quantity indicates flatness (for
negative values) or peakedness (positive values) of the pdf. The
are
the components of the real-space metric tensor. Note that 
,
i.e., (3.1.64) is an extension of eq. (2.2.53). Similarly,
vector invariants may be calculated for odd-order terms,
giving the direction of maximal skewness. Partial contraction of even-order terms,
reveals the directions of flatness and peakedness.
Various discussions in the literature (see, e.g., Kuhs, 1992, and references therein) indicate that the Gram-Charlier formalism is the best choice in routine crystallographic work. In particular, it has the advantage that the reverse Fourier transformation (1.4.8) can be carried out analytically,
with 
Hermite polynomials, and
the harmonic part of the pdf.
These polynomials are
tabulated by Johnson & Levy (1974) up to the fourth order and by Zucker &
Schulz (1982) up to the sixth order [see also Coppens (1993)]. The use of the
Gram-Charlier expansion (3.1.62) is therefore recommended, although other
formalisms may sometimes be advantageous for special problems. In any case,
the results should always be carefully checked, especially if higher order
terms are used merely to improve the agreement of the fit. Strong and extended
negative regions in the pdf indicate inadequacy of the results. One also has
to remember that, with anharmonic refinements, the positions and
obtained are not necessarily faithful representations of the mean and
variance of the pdf, respectively. This must be borne in mind if bond
distances and Gaussian displacement ellipsoids are to be derived
from the refined parameters. In some situations, it may be better to
use only the Gaussian approximation, even
though the resulting R-factors may be higher.
, which in the
classical limit
[ 
] is related to the pdf by Boltzmann statistics
with Z the partition function. The second equality is obtained by
setting 
.
The latter approach was formulated by Dawson & Willis (1967) and Willis (1969) for cubic point groups and later generalized for any symmetry by Tanaka & Marumo (1983). The OPP is written as
with 
the harmonic (quadratic) OPP and 
and 
the third and fourth order
coefficients, respectively, which are defined in a Cartesian system. Since
application of eqs. (3.1.68) and (1.4.8) does not lead to an
analytical expression for , the anharmonic part 
is approximated in (3.1.68) by
The final expressions for 
are rather lengthy and may
be found in Tanaka & Marumo (1983). Refinable parameters are the
and . Other formulations with
simpler expressions for have been introduced by Coppens
(1978), Kurki-Suonio, Merisalo & Peltonen (1979) and Scheringer (1985). None
of these approaches seems to have been used much in crystallographic
studies, and final recommendations must await further developments in
this field. It should also be noted that the OPP approach treats each atom
as an individual
(Einstein-)oscillator, which is a poor approximation for tightly bound
atoms in molecules.
The OPP approach is physically meaningful only for purely dynamic displacive
disorder (giving, e.g., the directions of weak and strong bonds), and is
limited to rather small anharmonicities through the approximation
(3.1.70). Occasionally special expansions (e.g.,
symmetry-adapted spherical harmonics) of pdf(u) or
have been used for special problems (e.g., curvilinear
motion, molecular disorder); see Johnson & Levy
(1974), Press & Hüller (1973) and Prandl (1981). Again, these expansions
do not seem yet to have entered routine crystallographic work. It should
be remembered that the classical limit , which is
assumed in eq. (3.1.68),
may be far from the actual situation even at room temperature.
and
should
always be superscripted when the refinement is referred to a crystal system
rather than to a Cartesian system. This definition follows from the
definition of the elements of and
as contravariant tensor components (see Section 2.1, p. 11). The frequent
use of subscripts for the ADPs, and specifically for those not referred to
Cartesian systems, is inconsistent with their tensorial properties. , which have dimension
(length)2, defined in eq. (
2.1.25), or the
dimensionless , defined in eq. (2.1.22). and are defined in eq. (2.1.26).
These quantities are directly proportional to the
recommended , the ratio being 8 .
instead of 
, for programming
convenience. This was possible because the matrix representing the ADP is
symmetric, with only six independent terms. This practice is not found
in modern crystallographic software. should always be accompanied by their standard
uncertainties. The ratio of the minimum to the maximum eigenvalues of the
corresponding anisotropic displacement tensors should also be published,
either in the primary publication itself or in the secondary (deposition)
publication. Authors of crystallographic software and crystallographers who maintain their own software are encouraged to introduce the minor modifications that are required for the implementation of these Recommendations.
This document contains the whole ADP Report as a single entity, with internal links referring to equation numbers alone. In order to access the same document with extensive hyperlink sectioning and cross-references, please click here.
ADP Report Webmaster
